One Way to Increase Follower Count

One common tip that streamers get when trying to gain more Twitch followers is to stream frequently. Some sources such as Lifewire suggest streaming 5 hours a day is a quick way to gain followers. With data of the top 1,000 Twitch streamers in the world being available on Kaggle, I wanted to check to see if there truly is a positive relationship between streaming more frequently and an increase in follower count.

Examining the Data

The data provided by Kaggle gives us basic data from the top 1,000 Twitch streamers, updated as recently as of February 2020. As the image below shows, we get data ranging from channel name to what language the channel is in.

Here is a key to see exactly what each column header(variable) is:

• Channel: The streamer’s channel name
• Watch time(Minutes): The total amount of time that the streamer has been watched on stream (in minutes)
• Stream time(minutes): The total amount of time the streamer streamed to their audience (in minutes)
• Peak viewers: The max amount of viewers they had at once during a stream
• Average viewers: The average amount of viewers they had during a stream
• Followers: The total amount of followers they currently have (as of February 2021)
• Followers gained The amount of followers gained during February 2020 - February 2021
• Views gained: The amount of views gained during February 2020 - February 2021
• Partnered: If they are an official Twitch partner
• Mature: If the streamer has voluntarily (usually) set their channel to mature, meaning they tell users that there could be profanity, etc
• Language: What language the streamer mainly streams in

In order to work with the data, I cleaned the data by replacing spaces in the column headers with underscores. This is to prevent any bugs within my code when creating linear regression models down the line. I also feature engineered new variables, “Stream_time_hr” and “Stream_time_days”, in order to make reading the stream time data more digestible.

So Now What?

After I cleaned up my data, I started to think of what methods would be best to prove that there is a relationship between streaming often and gaining followers. I decided to take a step-by-step process, using the more simplistic methods first, and then expanding to more elaborative methods at the end. This would hopefully allow me to craft a better picture of the relationship between the variables while also showcasing multiple methods in the process. The methods that I used in order were:

• 2-independent-sample t-test
• Simple linear regression model
• Simple linear regression model with outliers removed
• Multiple regression model

I will go into more detail of each method as we proceed.

Using a 2-Independent-Sample T-Test

The first method, and perhaps the most simplest method I used was a 2-independent-sample t-test. This method checks to see if two population means(averages) are equal. Or specifically for this case, it checks to see if the mean of followers_gained for streamers who stream a lot is equal to the mean of followers_gained for streamers who don’t stream a lot. This is called the null hypothesis. There is also an alternate hypothesis where it says the population means aren’t equal. We test to see if we can reject or fail to reject the null hypothesis or accept the alternate hypothesis. You can find the null and alternate hypothesis below:

• H0:μ_streamers who stream a lot_=μ_streamers who don’t stream a lot_

• Ha:μ_streamers who stream a lot_≠μ_streamers who don’t stream a lot_

However in order to conduct this test, we would need to classify how many hours is considered a lot for streamers. Using the baseline provided by Lifewire of 5 hours a day, we can estimate that streamers who stream a lot probably stream 5 hours a day, or more than 1303.57 hours a year. So I feature engineered another variable “Streams_a_lot”, which assigned a 0 to streamers who didn’t stream more than 1303.57 hours a year and a 1 to streamers who streamed more than 1303.57 hours a year.

I then conducted the t-test using the variables “Streams_a_lot” and “Followers_gained” to see if there is a relationship between them. Using Python, I calculated the P-value to be 1.28e-07, which was below the standard significance level of 0.05. Therefore we could reject the null hypothesis and conclude that there is indeed a relationship between streaming a lot and gaining followers.

Diving Deeper with a Simple Linear Regression Model

One of the limits of using a t-test is that it only tells us that there is a relationship between two variables. If we wanted to learn how statistically related two variables are we could use a Simple Linear Regression Model. This model compares the linear relationship between two continuous variables. So in this model, we would use the quantitative variable “Stream_time_hr” as our independent variable, instead of “Streams_a_lot” since “Streams_a_lot” is a categorical variable. Our dependent variable would still be “Followers_gained”. And our null hypothesis will be slightly different as although it still tests that the two variables are unrelated, it also mathematically tests that the slope between these two variables are equal to zero.

• Ho: β1=0
• Ha: β1≠0

In order to see the simple linear regression model, I plotted our two variables against each other in Python

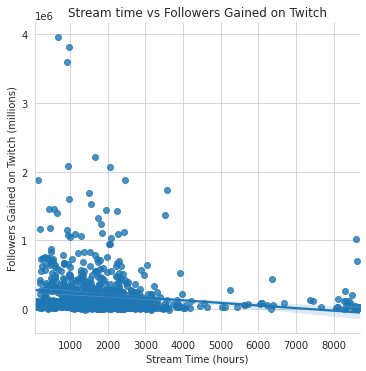
Just by looking at the graph, I could see that there is a negative correlation between the two variables. However since the axis for “Followers_gained” is in the millions, it’s hard to say how strong the correlation is, but it still looks a little bit on the weaker side. We could also see a bit of outliers in the graph, which could skew the correlation to be more negative. The data points also seem pretty spread, however since there are 1,000 data points, it could be deceptively more linear than it looks.

Now that we know how the model looks, we could use Python to calculate the P-value and R-Coefficient(linear correlation coefficient). The R coefficient measures the strength and direction of the linear relationship between two quantitative variables.

from scipy import stats

r_st_fg, p_val_st_fg = stats.pearsonr(df['Stream_time_hr'], df['Followers_gained'])

print('R Coefficient: ', r_st_fg)
print('P-Value: ', p_val_st_fg)

The resulting code shows us that the P-value is 4.98e-07 and the R coefficient to be -0.158. So since this P-value is less than 0.05, we would reject our null hypothesis that there is no relationship between the two variables. This confirms what we already know from the t-test before. Additionally the R coefficient shows us that there is a weak, negative correlation between the variables. This confirms what we saw in our graph but it also shows contrary to what Lifewire said about the relationship between streaming time and gaining followers. Instead of seeing an increase of followers with streaming time, we see a decrease of followers with streaming time. However, there are still a few more models to execute before we make a conclusion.

We could also use Python use the ols model from statsmodels to find us the details of the linear regression

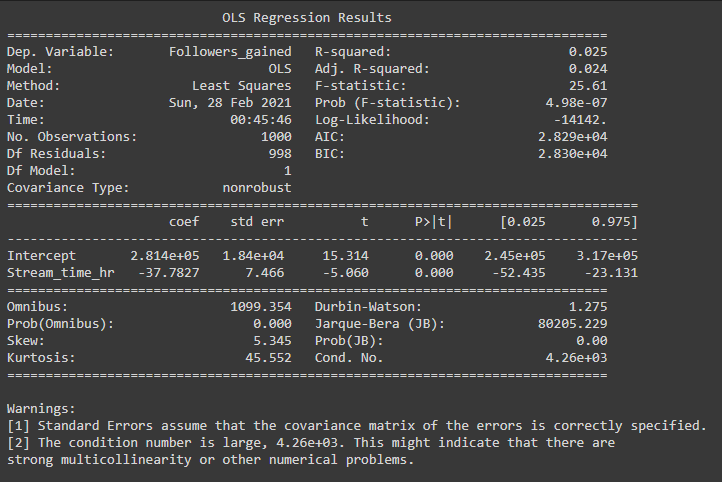
The main components to look at in this model are

• Stream_time_hr: This shows the slope of the graph. For every one unit increase in Stream_time_hr, Followers_gained decreases by 37.78
• R-Squared: the percent of the variability in the y variable that is explained by differences in the x variable

The most important component to get from this model is R-Squared. It basically says that 2.5% of the variability seen in Followers_gained is explained by Stream_time_hr. This value is pretty low and shows that there are either a better model to fit the data, or there are other factors affecting the data, whether it be outliers or other data points that we aren’t looking at. This confirms that we should make changes in our model to find a more fitting model.

Lets Remove Some Outliers

Looking at the graph before, visually it looked like there were some outliers in the data. For instance, looking at the “Stream_time_hr”, when calculating the numbers, we could see that some of the streamers were live for 365 days of the year. This essentially means that these channels stayed live for every hour of the year, and therefore the channels content was very atypical compared to the average channel content. A lot of these channels would just stream movies for viewers to watch, without the actual streamer being present. Therefore, in order to find the outliers, we used the df.describe function to find the interquartile range(IQR) for our variables.

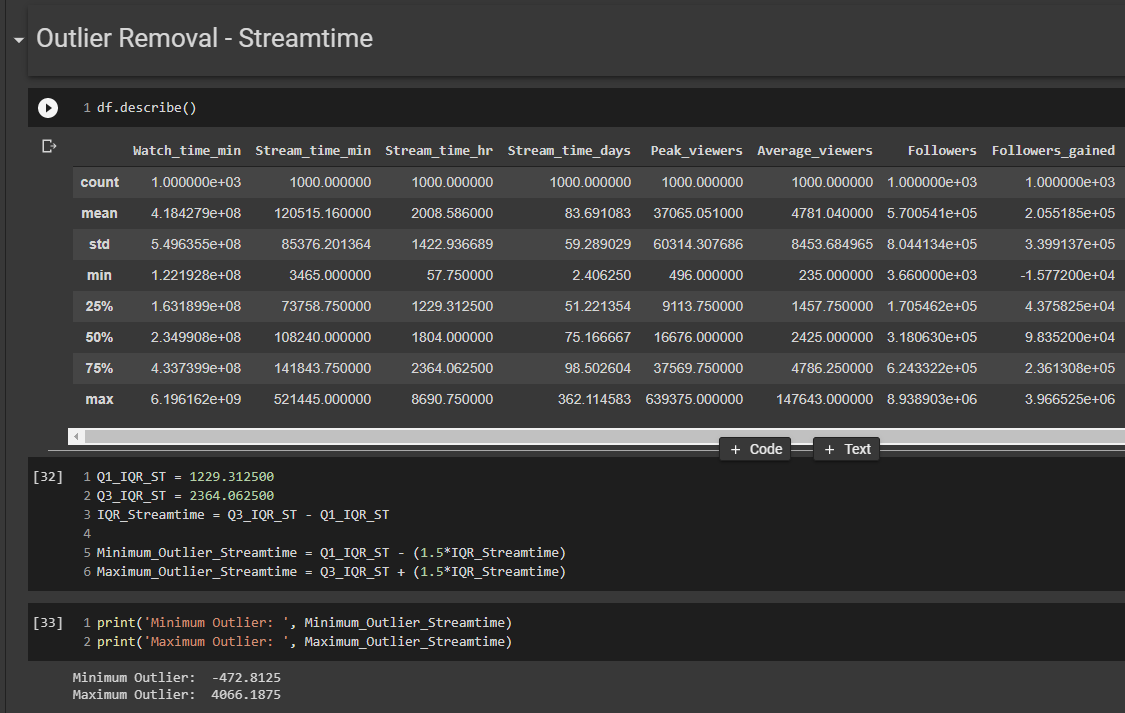
Using the IQR, we can calculate our outliers, and then remove them from a copy of our data. Then we do another simple linear regression model, except this time with the data with our outliers removed.

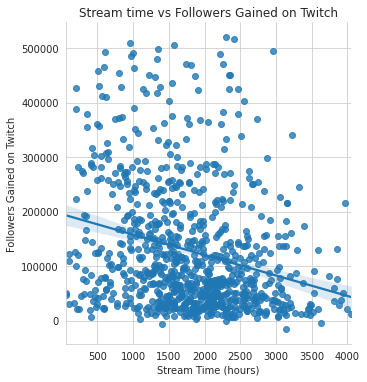
Although the data looks more spread out, it’s interesting to note that the axis ranges have significantly reduced. In particular, “Followers_Gained” reduced from 1,000,000 to 500,000 people. So technically, it should be that there should be an increase in correlation and hopefully R-Squared value.

After running the OLS model from Python we found our values to be:

• P-Value: 1.33e-14
• Linear Correlation Coefficient: -0.258
• R-Squared: 0.067

Looking at these numbers, we can see that the linear correlation coefficient has become stronger from -0.158 to -0.258. However since it got stronger in the negative direction, it’s starting to look more likely that our data won’t support Lifewire’s claim. The R-Squared value slightly increased too, however overall, it is still very low at 6.7%. It looks like that it would be worth looking at some more models.

Adding New Variables to the Model Helps

With such a low R-Squared value, we could probably improve our model if do a multiple regression model with added variables. Just looking at the data we have, some variables that could help improve the model are “Followers”, “Watch_time_min”, “Partnered”, “Peak_viewers”, and more. I played around with adding different variables into the OLS model to see which combination of variables have the best fit, and using the data with the outliers removed, I found that the strongest combination of variables that we have are “Followers_gained”, “Stream_time_hr”, Followers, and “Watch_time_min”.

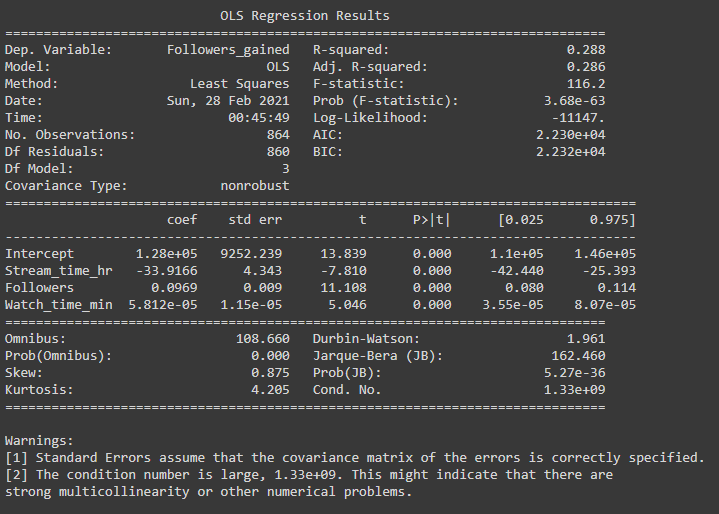
For the multiple regression model, there is no true linear correlation coefficient since we are using multiple variables in the model. Therefore there can’t just be one line to connect all the variables since we are technically using four variables in our model. However. looking at the slope of “Stream_time_hr”, we find that it is still negative, so we can still infer that there is a negative correlation between “Stream_time_hr” and “Followers_gained”

And we also found that the Adjusted R-squared value increased to 0.286 compared to the 0.067 we had before. Or in other words, 28.6% of the variability in “Followers_gained” can be explained by the variables “Stream_time_hr”, Followers, and “Watch_time_min”. Although the R-squared value increased by a lot, overall it still isn’t the highest. This means that we need to find more data (either increase the number or variables or sample size) or find a better fitting model instead of a linear regression. To note, I also tried using logistic regression to see if that better fit the data, but that didn’t improve the fit. Given more time, I would look into other mathematical models that could help improve our data.

So, Streaming More Often Doesn’t Help Gain More Followers?

Therefore, it seems that Lifewire and other sources claims were wrong and that streaming more often doesn’t help streamers gain more followers. However, before we make any definite conclusions, we still have to look at the context of the data that was used in all our models. Firstly, the data from Twitch that we received only contained data from the Top 1000 streamers on Twitch. And although the data encompasses streamers who aren’t the most impressive holistically (the smallest streamer in our dataset averages 235 viewers), it is still a very small and biased minority of the streamer community. These streamers are still at the top of the streaming ecosystem, and it is likely that different trends occur at the top compared to streamers just starting out. Also, there are many more smaller streamers in the streaming ecosystem, who not only are on Twitch, but on other platforms like Facebook, YouTube, and more. If we wanted to make less biased models, we would need a random sampling of all streamers on all streaming platforms (or better data for our models include all data of all streamers on all streaming platforms).

Also, it seemed that Lifewire’s advice was primarily targeting aspiring streamers. So if our data included only all streamers who started in the past year, we might be able to get different results that support Lifewire’s claim that streaming more helps streamers gain more followers. In the future, if that data is available, I would re-run the models with this data to see if there is a difference.

We also have to acknowledge that there are many unknown factors that help a streamer grow, and some of those factors may not even be able to be recorded into data as of yet. For instance, some streamers blow up depending on their network connections. Or other streamers grow significantly because they excelled at streaming the newest gaming trend. As more variables of data are able to become recorded, we could create more accurate models to see how correlated certain variables are to gaining followers.

However, in conclusion, we found that within the top 1000 streamers on Twitch, streaming more often is correlated negatively with gaining followers. Or top Twitch streamers who streamed more often, would often not gain as many followers as top Twitch streamers who streamed less often.